This proof will follow the discussion before the statement of the theorem. Mostly, we will just fill in some details and provide some further justification for why what we were noticing must be true.
Let’s start with the conditions of the test:
-
We are considering an
Alternating Series,
\(\displaystyle \sum_{k=0}^\infty a_k\text{.}\) For our purposes, we’ll assume that we have something like
\begin{equation*}
\sum_{k=0}^\infty a_k = |a_0| - |a_1| + |a_2| - |a_3| +-...
\end{equation*}
where the even-indexed terms are the positive ones. This could be flipped and it wouldn’t make a difference.
-
The size of the terms are decreasing. That is,
\(|a_k|\lt |a_{k+1}\) for all
\(k=0,1,2,...\)
-
The limit
\(\displaystyle\lim_{k\to\infty} a_k=0\text{.}\) Note that this also means that
\(\displaystyle\lim_{k\to\infty} |a_k|=0\text{.}\)
We’re going to show that, under these conditions, the alternating series we’re considering must converge. The way that we’ll do this is, no surprise, by invoking
Theorem 8.1.10 Monotone Convergence Theorem. We’re going to do it by considering the partial sums in halves: the even-indexed ones and the odd-indexed ones.
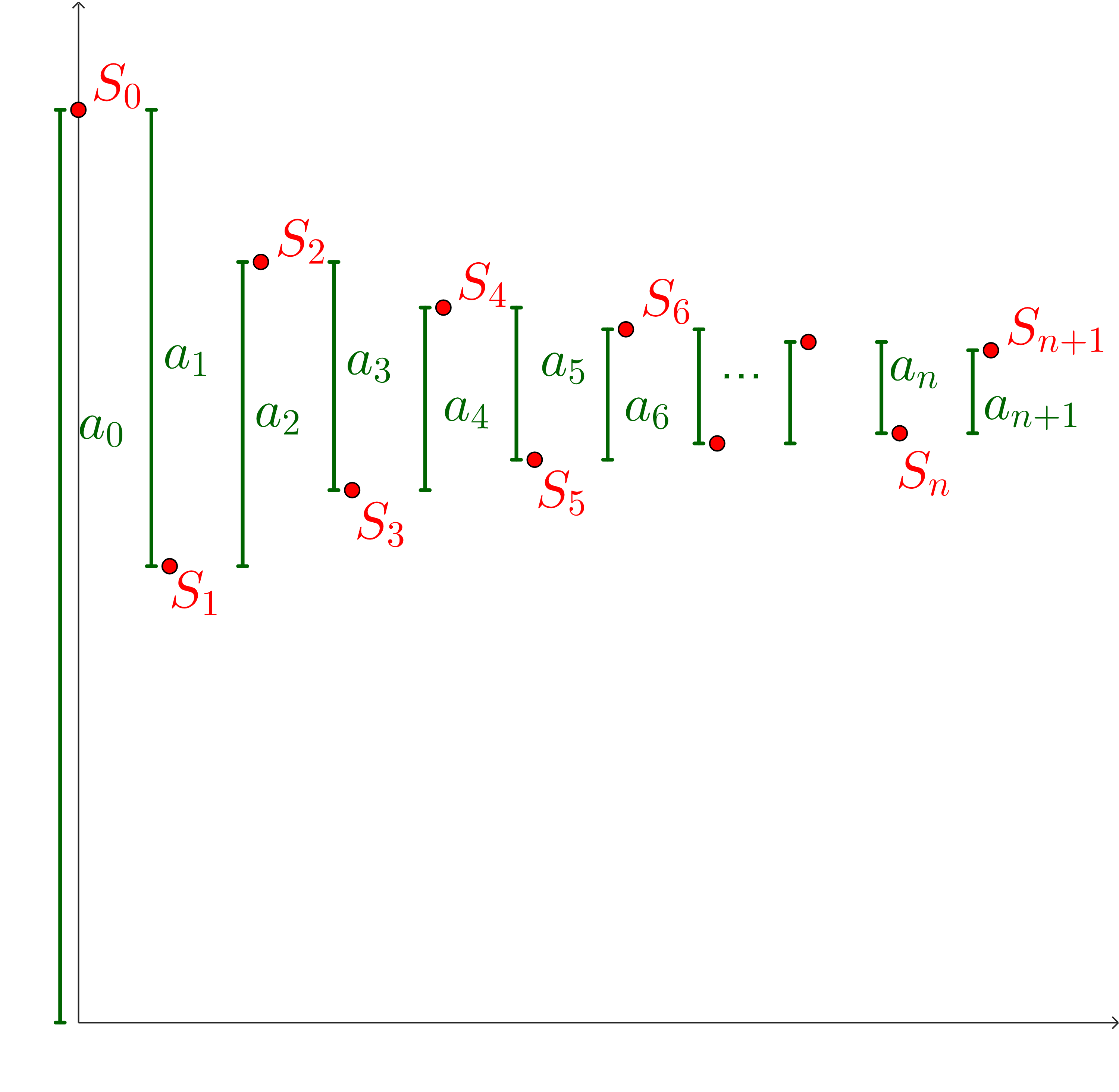
First, consider the sequence \(\{S_{2n}\}_{n=0}^\infty = \{S_0, S_2, S_4, ...\}\text{.}\) The difference between successive terms in this sequence (successive even-indexed partial sums) is:
\begin{equation*}
S_{2n+2} - S_{2n} = -|a_{2n+1}| + |a_{2n+2}|\text{.}
\end{equation*}
Since the terms of the alternating series are decreasing in size, we know that \(|a_{2n+2}|\lt |a_{2n+1}|\text{,}\) which means that \(S_{2n+2}-S_{2n}\lt 0\text{,}\) and so \(S_{2n} \gt S_{2n+2}\text{.}\)
All of this which is to say,
\(\{S_{2n}\}_{n=0}^\infty\) is a decreasing sequence.
We can apply the same reasoning to the sequence \(\{S_{2n+1}\}_{n=0}^\infty = \{S_1, S_3, S_5, ...\}\text{.}\) We know the differences between successive odd-indexed partial sums is:
\begin{equation*}
S_{2n+3} - S_{2n+1} = -|a_{2n+3}| + |a_{2n+2}|\text{.}
\end{equation*}
This time, though, \(|a_{2n+2}|\gt |a_{2n+3}|\) and so the difference is positive: \(S_{2n+3} - S_{2n+1}\gt 0\) which means that \(S_{2n+3} \gt S_{2n+1}\text{.}\) The sequence \(\{S_{2n+1}\}_{n=0}^\infty\) is an increasing sequence.
We’re getting close! We have monotonic sequences. Now we just need to show bounds, and then we’ll show that each of these sequences converges. Then, we’ll show that they converge to the same thing.
Getting an upper bound on the odd-indexed partial sums and a lower bound on the even-indexed partial sums is pretty easy. Let’s consider subsequent partial sums, \(S_{2n}\) and \(S_{2n+1}\text{.}\)
\begin{align*}
S_{2n+1} - S_{2n} \amp =-|a_{2n+1}|\\
S_{2n+1} - S_{2n} \amp \lt 0\\
S_{2n+1} \amp \lt S_{2n}
\end{align*}
Ok so this is easy: we can just pick any odd-indexed partial sum to be the lower bound on the even-indexed partial sums, and vice versa.
So \(S_0\) is an upper bound on \(\{S_{2n+1}\}_{n=0}^\infty\text{,}\) since every other \(S_{2n}\) is less than \(S_0\text{,}\) and all of \(S_{2n+1}\) partial sums are less than \(S_{2n}\text{:}\)
\begin{align*}
S_0 \amp \geq S_{2n} \amp \text{for } n=0,1,2,... \\
S_0 \amp \geq S_{2n} \gt S_{2n+1} \amp \text{for } n=0,1,2,... \\
S_0 \amp \gt S_{2n+1} \amp \text{for } n=0,1,2,...
\end{align*}
Similarly, we can say the same thing about \(S_1\) being a lower bound for the even-indexed partial sums:
\begin{align*}
S_1 \amp \leq S_{2n+1} \amp \text{for } n=0,1,2,... \\
S_1 \amp \leq S_{2n+1} \lt S_{2n} \amp \text{for } n=0,1,2,... \\
S_1 \amp \lt S_{2n} \amp \text{for } n=0,1,2,...
\end{align*}
So we have shown that the sequences
\(\{S_{2n}\}_{n=0}^\infty\) and
\(\{S_{2n+1}\}_{n=0}^\infty\) are both monotonic and bounded and so both of these sequences must converge.
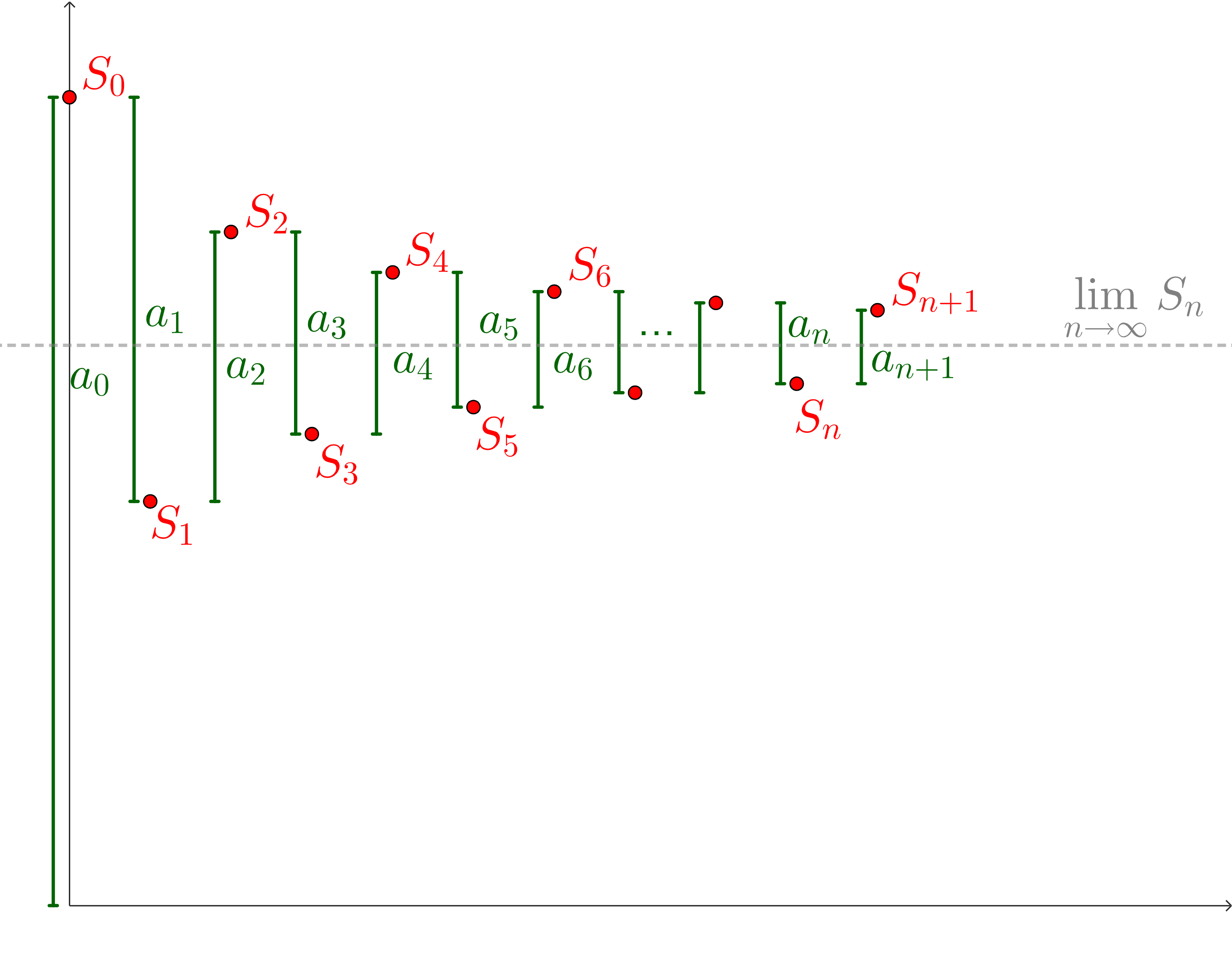
Now we can show that they converge to the same thing.
Since \(\{S_{2n}\}_{n=0}^\infty\) converges, let’s say that there is some number \(S_E\) where
\begin{equation*}
\lim_{n\to\infty} S_{2n} = S_E\text{.}
\end{equation*}
Similarly, there is a number \(S_O\) where
\begin{equation*}
\lim_{n\to\infty} S_{2n+1} = S_O\text{.}
\end{equation*}
Now we can use the fact that the limit of the terms is 0:
\begin{align*}
\lim_{k\to\infty} a_k \amp=0 \\
\lim_{n\to\infty} a_{2n+1} \amp =0\\
\lim_{n\to\infty} \left(S_{2n+1}-S_{2n}\right) \amp=0 \\
S_O-S_E\amp=0
\end{align*}
So the numbers that these two sequences of partial sums converge to are actually equal to each other.
So, finally, we know that under the conditions we started with, the alternating series must converge.