Other Applications of Integrals

Section 6.6 Other Applications of Integrals

We should pause and think (even briefly) about the whole point of this chapter.

🔗

Do you think you will need to know how to calculate the volume of a solid of revolution?

🔗

Is being able to think about the surface area of a solid of revolution important?

🔗

Are you going to need to calculate a bunch of arc lengths constantly in your other classes, jobs, or spare time?

🔗

No. Probably not. It’s fun to think about this stuff, but the goal is not really the formulas: it’s the construction.

🔗

What we really should be leaving this chapter with is a renewed view of what a definite integral is. After Chapter 5 Antiderivatives and Integrals, we probably thought about a definite integral as a measurement of the (signed) area “under the curve” (bounded between the curve and the \(x\)-axis). Hopefully now, though, we have a deeper view of the definite integral through this slice-and-sum process.

🔗

A definite integral is an accumulation of some function outputs multiplied by the space between the inputs.

🔗

So when we do move past these topics into other classes, jobs, or your spare time, then you will run into formulas involving definite integrals. Hopefully, based on this chapter, we have the tools to deconstruct those formulas to find out what they are measuring and how they are measuring it.

🔗

To end the chapter, let’s look at some applications of definite integrals into formulas from other academic fields.

🔗

Subsection Physics Application: Mass

Let’s consider some object made out of a material with a constant density. To calculate the mass of the object, we need to know the size (the volume of the object) and the density, and then we can multiply:

\begin{equation*} \mathrm{mass} = \mathrm{density} \cdot \mathrm{volume}\text{.} \end{equation*}

We’ve seen how we can use the slice-and-sum formula to calculate volumes by slicing the object into thin pieces and approximating the volume by multiplying the cross-sectional area by the thickness of the slice:

\begin{equation*} V_k = A(x_k^*) \Delta x\text{.} \end{equation*}

We can easily construct an integral formula for the mass of an object now! We just need to find some measurement of the mass of a single slice of an object, and then start summing until we end up with a definite integral! So, for an object spanning from \(x=a\) to \(x=b\) with density, \(\rho\text{,}\) we have:

\begin{align*} M_k \amp = \rho V_k\\ \amp = \rho A(x_k^*)\Delta x\\ M \amp \approx \sum_{k=1}^n \rho A(x_k^*)\Delta x\\ M \amp = \lim_{n\to\infty}\sum_{k=1}^n \rho A(x_k^*)\Delta x\\ \amp = \int_{x=a}^{x=b} \rho A(x)\;dx \end{align*}

This is great! We can easily extend this to other situations, as well.

🔗

Imagine if the density of our object isn’t constant. Maybe we have some metal alloy, where the mixture of the metal changes as we traverse through the object. This variable density can be represented, then, as \(\rho(x)\text{.}\) We can replace the constant \(\rho\) with \(\rho(x_k^*)\) and then eventually \(\rho(x)\) to get:

\begin{equation*} M = \int_{x=a}^{x=b} \rho(x) A(x)\;dx\text{.} \end{equation*}

🔗

Theorem 6.6.1. Mass of an Object.

For some solid spanning from \(x=a\) to \(x=b\) where \(A(x)\) is the cross-sectional area of the object at \(x\) and \(\rho(x)\) is the density of the object at \(x\text{,}\) then the total mass of the object is:

\begin{equation*} M = \int_{x=a}^{x=b} \rho(x) A(x)\;dx\text{.} \end{equation*}

🔗

For very thin objects, like wires, we can not consider the cross-sectional area and simply use what we call the linear density: \(\rho(x)\) measures the amount of mass per unit length (instead of mass per cubic unit of volume). In this case, our formula changes.

🔗

Theorem 6.6.2. Mass of a Thin Wire.

For some thin object (like a wire) spanning from \(x=a\) to \(x=b\text{,}\) then if \(\rho(x)\) measures the mass per unit of length (\(\rho(x)\) is a linear density function), then the mass of the object is:

\begin{equation*} M = \int_{x=a}^{x=b} \rho(x)\;dx\text{.} \end{equation*}

🔗

Example 6.6.3.

For each of the following objects, set up an integral expression to calculate the mass. Evaluate the integrals!

🔗

(a)

A thin wire that is \(30\) cm long with a density function \(\rho(x) = 2 + \frac{x}{60}\text{,}\) where \(\rho(x)\) measures the density of the wire at \(x\) in g/cm.

🔗

Solution.

\begin{align*} M \amp = \int_{x=0}^{x=30} \left(2+\frac{x}{60}\right)\;dx\\ \amp = \left(2x+\frac{x^2}{120}\right)\bigg|_{x=0}^{x=30}\\ \amp = 60 + \frac{900}{120}\\ \amp = 67.5 \end{align*}

The mass of the wire is \(67.5\) g.

🔗

(b)

A thin wire that is \(100\) cm long, with an unknown density. We assume that the density changes linearly from one end to the other, with the measured density at both ends being \(5.1\) g/cm and \(4.7\) g/cm.

🔗

Hint.

Construct the density function using two points: \((0,5.1)\) and \((100, 4.7)\text{.}\) You could switch the orders and use \((0,4.7)\) and \((100,5.1)\) as well. What is the linear function connecting these points?

🔗

Solution.

We’ll use the points \((0,5.1)\) and \((100, 4.7)\) to construct \(\rho(x)\text{.}\)

\begin{align*} \rho(x) \amp = \left(\underbrace{\frac{4.7-5.1}{100-0}}_{\text{slope}}\right)(x-0)+5.1\\ \amp = -0.004x+5.1 \end{align*}

Now we can integrate:

\begin{align*} M \amp = \int_{x=0}^{x=100} 5.1-0.004x\;dx\\ \amp = (5.1x - 0.002x^2)\bigg|_{x=0}^{x=100}\\ \amp = 510-20\\ \amp = 490 \end{align*}

So the mass of the wire is \(490\) g.

🔗

Subsection Physics Application: Work

Another example of a measurement found in physics contexts is Work. Work is, generally, the amount energy transferred to (or from, depending on perspective) an object by some force across some distance or displacement.

\begin{equation*} \mathrm{Work} = \mathrm{Force} \cdot \mathrm{distance} \end{equation*}

In general, we can use the “slice-and-sum” process when the force applied to our object is some function of the position:

\begin{align*} W_k \amp = F(x_k^*) \Delta x \\ W \amp \approx \sum_{k=1}^n F(x_k^*) \Delta x\\ W \amp = \lim_{n\to\infty} \sum_{k=1}^n F(x_k^*) \Delta x\\ \amp = \int_{x=a}^{x=b} F(x)\;dx \end{align*}

🔗

Theorem 6.6.4. Work Required.

If \(F(x)\) is a function measuring the force applied to an object at some \(x\)-value in the interval \([a,b]\text{,}\) then the work done to move the object across the interval is:

\begin{equation*} W=\int_{x=a}^{x=b} F(x)\;dx\text{.} \end{equation*}

🔗

In many contexts, we can notice that the force being applied to the object is dependent on the position of the object along its path. For instance, in the 1600’s, British physicist Robert Hooke claimed (and proved) that the force required to stretch or compress a spring is directly proportional to the distance that it is away from “equilibrium” (the position the spring naturally rests in).

🔗

Subsubsection Work: Springs

🔗

What if we pump liquid out of the top of a tank? How does that work? There are some fun things to think about. Let’s visualize this tank below, and then talk through the construction of the formula.

🔗

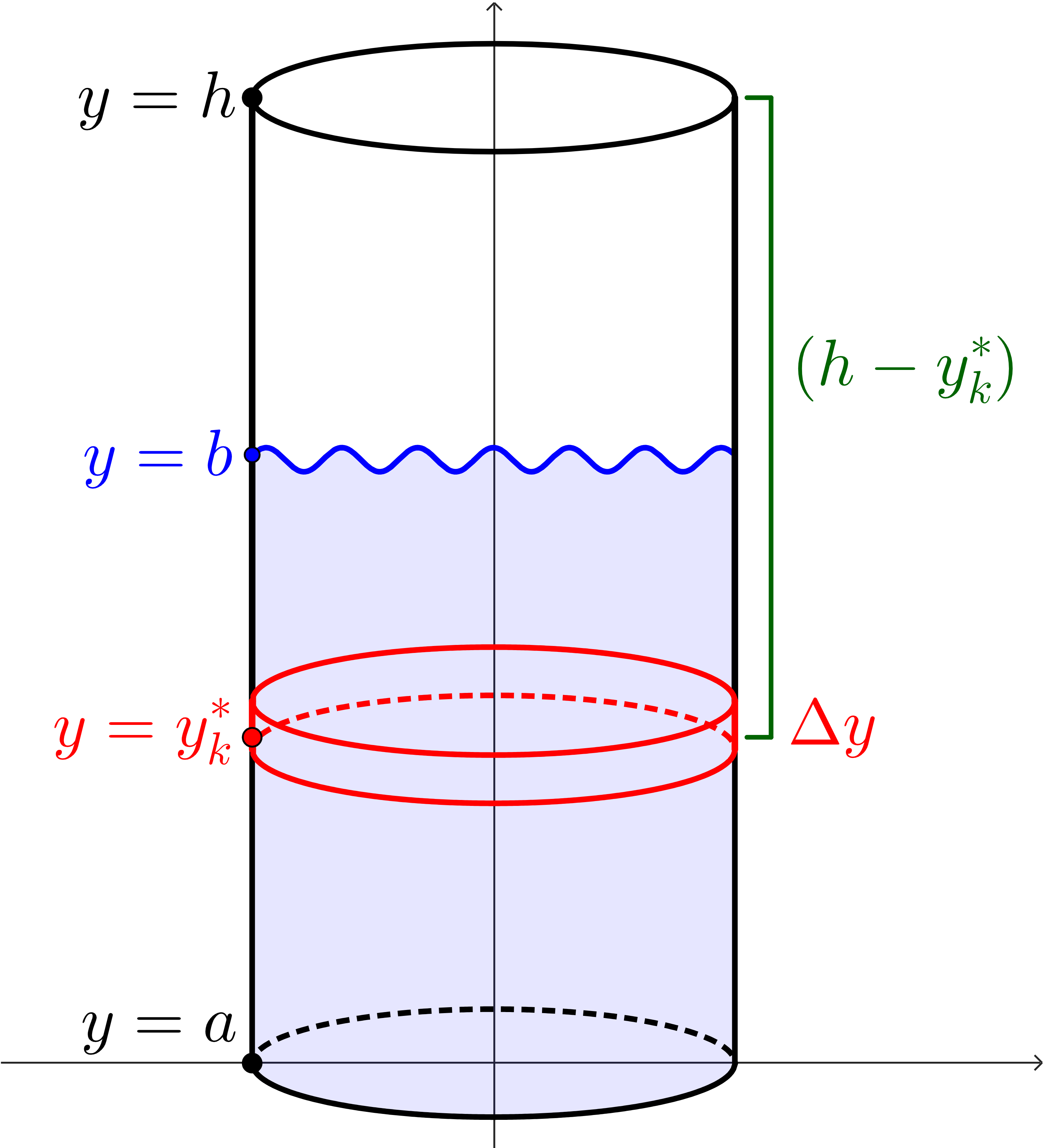
(for accessibility) — Figure 6.6.6. Diagram of a pumping problem.
🔗

We can see a couple of notable things here:

We’re going to slice up the liquid. So from \(y=a\text{,}\) the bottom of the tank, up to \(y=b\text{,}\) the height at the top of the volume of liquid, we will create \(k\) slices (each at some \(y_k^*\) \(y\)-value) with \(\Delta y\) representing the thickness of the slice.
🔗

🔗
The distance portion of the formula is not represented by the width of a subinterval from the whole distance. Instead, we’ll note that liquid at the top of the tank needs to be pumped a shorter distance than the liquid near the bottom of the tank. The distance part, then, is a function based on the \(y\)-value. So, if \(y=h\) is the height of the tank, then \((h-y_k^*)\) is the distance that the liquid in the \(k\)th slice will move.
🔗

🔗
To calculate the force required to pump the liquid in the \(k\)th slice, we need to know the mass of the liquid and the acceleration needed to pump the liquid out of the tank. The acceleration will be whatever the acceleration needed to overcome gravity: we’ll use \(g\text{,}\) the positive gravitational constant. For the mass, we’ll think about the density of the liquid (a constant, \(\rho\)) and the volume of the \(k\)th slice.
🔗

🔗
To find the volume of the \(k\)th slice, we’ll think about the cross-sectional area of the slice at \(y_k^*\) (we’ll call it \(A(y_k^*)\)) multiplied by the thickness, \(\Delta y\text{.}\)
🔗

🔗

This gives us the following in the slice-and-sum process:

\begin{align*} W_k \amp =F(y_k^*)(h-y_k^*)\\ \amp = \left(\rho A(y_k^*) \Delta y\right) g (h-y_k^*)\\ \amp = \rho g A(y_k^*) (h-y_k^*) \Delta y\\ W \amp \approx \sum_{k=1}^n \rho g A(y_k^*) (h-y_k^*) \Delta y\\ W \amp = \lim_{n\to\infty} \sum_{k=1}^n \rho g A(y_k^*) (h-y_k^*) \Delta y\\ \amp = \rho g \int_{y=a}^{y=b} A(y)(h-y)\;dy \end{align*}

So, when we consider these pumping problems, we really need to take note of only a few things:

What are the limits of integration? Where is the liquid we’re pumping (based on \(y\)-value heights)?
🔗

🔗
What is the geometry of our tank? When we consider a single slice of the liquid, what kind of shape will we have, and how do we calculate the cross-sectional area?
🔗

🔗

\begin{equation*} A(y) = \pi (3-1.5y)^2 \end{equation*}

The limits of integration are from \(y=0\) to \(y=1.5\text{:}\)

\begin{align*} W \amp = \rho g \pi \int_{y=0}^{y=1.5}(3-1.5y)^2(2-y)\;dy\\ \amp = \rho g \pi \int_{y=0}^{y=1.5}18 - 27 y + 13.5 y^2 - 2.25 y^3 \;dy\\ \amp = \rho g \pi \left(18y - \frac{27y^2}{2} + \frac{13.5y^3}{3} - \frac{2.25y^4}{4}\right)\bigg|_{y=0}^{y=1.5}\\ \amp = \frac{2295\rho g \pi}{256} \end{align*}

A frustum-shaped tank where the bottom radius is 4 m, the top radius is 1 m, the height is 2 m, and the tank is filled to a height of \(\frac{2}{3}\) m.

🔗

Prev Top Next