Skip to main content

Discover Calculus Single-Variable Calculus Topics with Motivating Activities

Peter Keep

Section 8.7 Comparison Tests

So far, our strategies for thinking about infinite series have been focused around drawing a connection between the infinite series we care about and some other mathematical object:
Now we’ll work on building the most important series convergence test mechanism: we’ll draw a link between the series we care about and some other series that we already know about.
🔗
This is helpful for three reasons:
  1. We already have a couple of types of series that we know about (Section 8.6), and we can keep adding to that list.
    🔗
    🔗
  2. We can take advantage of similar structure or common term formulas when we see them to essentially say, “This series kind of looks like one that I recognize. I wonder if they act the same?”
    🔗
    🔗
  3. We don’t always have to integrate things using the Integral Test! Integrating can be hard!
    🔗
    🔗
🔗

Subsection Comparing Partial Sums

We’re going to start by trying to do the same thing we did when we build the Integral Test: show that the partial sums are monotonic and bounded and then make use of the Monotone Convergence Theorem.
🔗

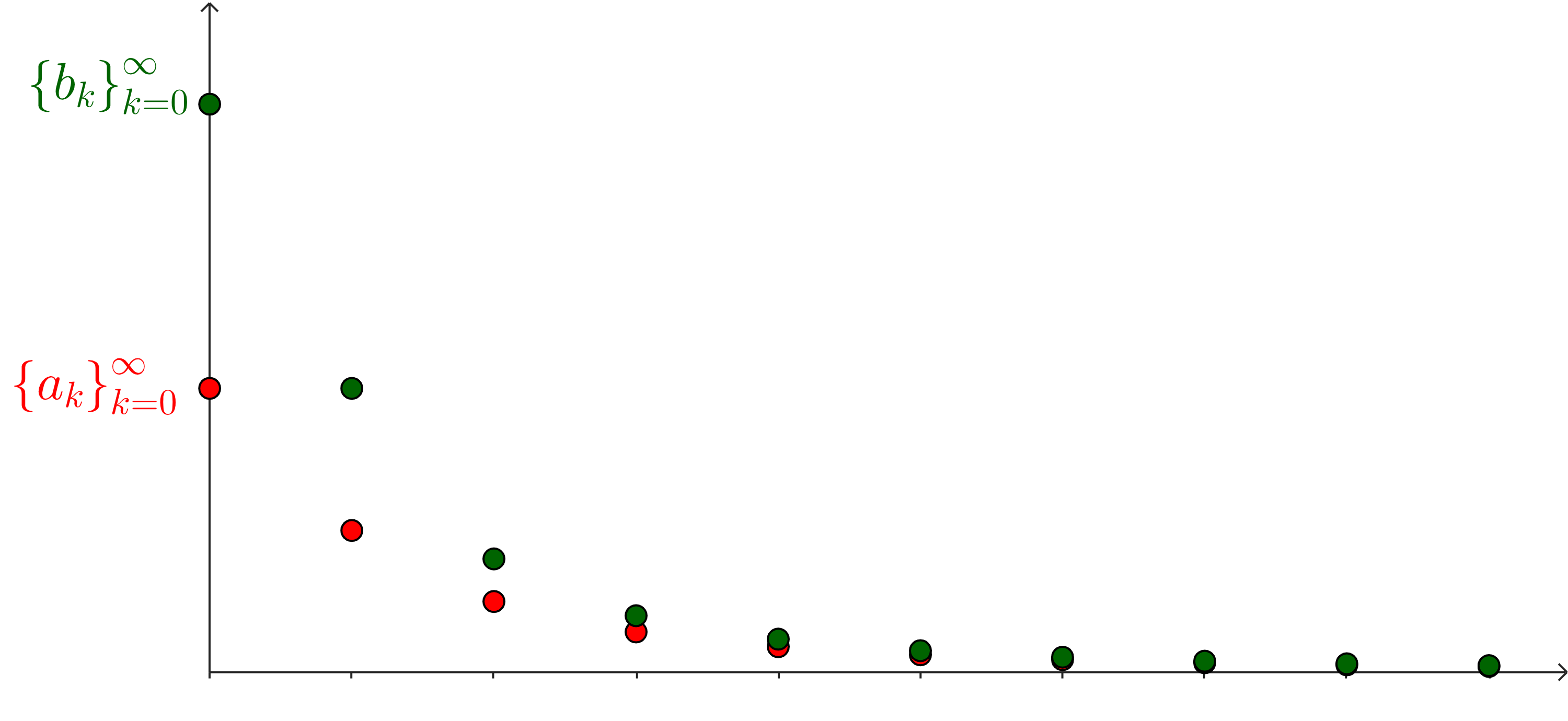
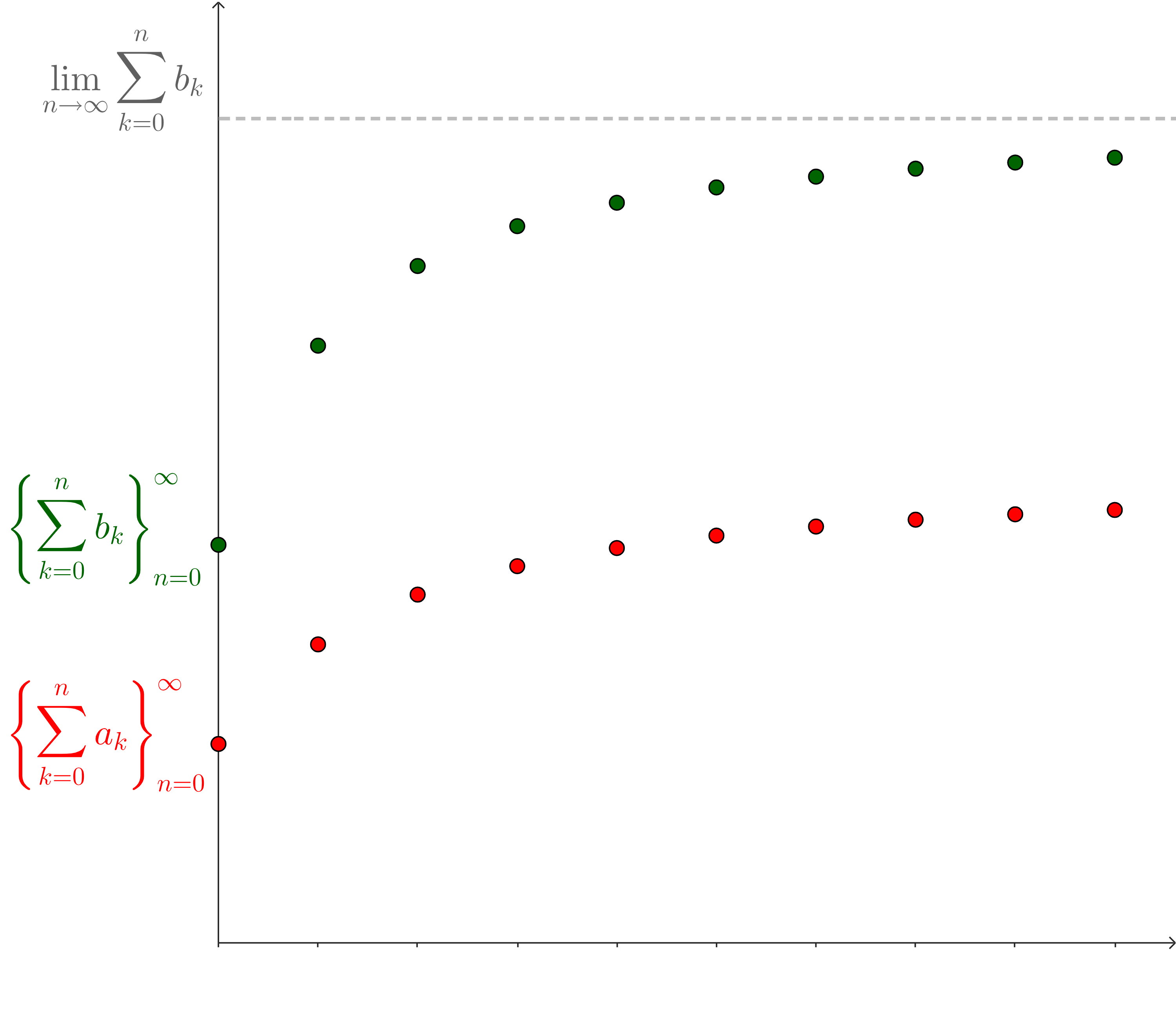
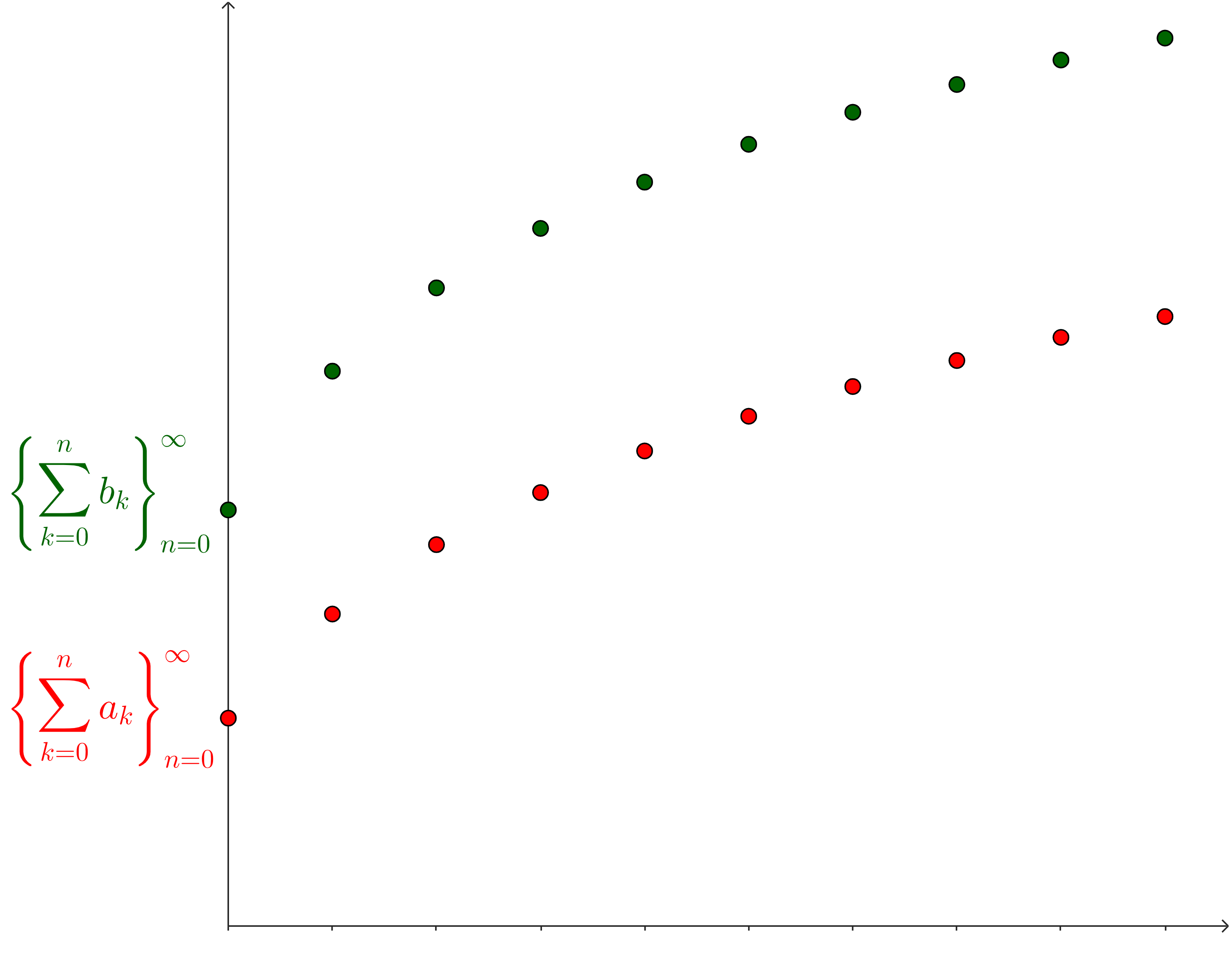
Activity 8.7.1. Comparisons to Bound Partial Sums.

This activity is mostly going to be thinking about proof mechanisms, and so it might be helpful to review Activity 8.4.1 Integrals and Infinite Series. If you want to see more, then the proof of Integral Test will provide some further details on why the inequalities we built were useful.
🔗
(a)
In the Integral Test, how did we guarantee that our sequence of partial sums was monotonic?
🔗
🔗
(b)
How did we know that, as long as the corresponding integral converged, then our sequence of partial sums was bounded?
🔗
🔗
(c)
How did we know that, as long as our integral diverged, then our sequence of partial sums had to diverge as well?
🔗
🔗
(d)
What happens if we swap out the integral we’re connecting our series to with a different series?
🔗
For these inequalities to be useful, what do we need to be true?
🔗
Hint 1.
For our sequence of partial sums to be bounded, we originally had that our partial sums were smaller than an expression involving an integral. Then, those integrals eventually converged to something, and so our sequence of partial sums was bounded by a value.
🔗
Can we swap out an integral for a different partial sum? What has to happen in the limit to guarantee that our series converges?
🔗
🔗
Hint 2.
Similarly, when we showed that our partial sums were always greater than something involving an integral, then we were able to show that if that integral diverged, then our partial sums had no choice but to diverge to infinity as well.
🔗
What kind of partial sum do you need to change out the integral for?
🔗
🔗
🔗
🔗
This is it! We have everything we need to construct another link: this time between the infinite series we care about and another infinite series that we think acts the same.
🔗
To illustrate what we’ve done, let’s think about two sequences of terms: \(\{a_k\}_{k=0}^\infty\) and \(\{b_k\}_{k=0}^infty\) where \(a_k\leq b_k\) for \(k\geq 0\text{.}\) We can think of the graphs, pictured below.
🔗
A sequence of green dots, labeled {b_k}, decreasing to the horizontal axis. There is a second sequence of red dots, labeled {a_k}, also decreasing to the horizontal axis. At some point, the green dots look like they’re on top of the red ones.
Figure 8.7.1. The “smaller” sequence of terms \(\{a_k\}_{k=0}^\infty\) graphed alongside the “bigger” sequence of terms \(\{b_k\}_{k=0}^\infty\text{.}\)
🔗
Now we can think about the graphs of these partial sums. Let’s first think about what might happen if the series \(\displaystyle \sum_{k=0}^\infty b_k\) converges. We’ll plot the partial sums, and the sequence of partial sums has to converge to something. But then we can think about the sequence of partial sums from the \(a_k\) terms: the smaller terms, of course, will build smaller partial sums.
🔗
A sequence of green dots, labeled {partial sum of b_k}, increasing to a horizontal line. The line is labeled as the limit of the partial sums of b_k. There is a second sequence of red dots, labeled {partial sums of a_k}, also increasing but below the green dots.
Figure 8.7.2. Comparison of partial sums when \(\displaystyle\sum_{k=0}^\infty b_k\) converges.
🔗
So we can pretty easily use \(\displaystyle\lim_{n\to\infty}\sum_{k=0}^n b_k\) as an upper bound on the sequence \(\displaystyle \left\{\sum_{k=0}^n a_k\right\}_{n=0}^\infty\text{!}\) And now we can say that the sequence of partial sums for \(\displaystyle \sum_{k=0}^\infty a_k\) is monotonic and bounded, and so it must converge.
🔗
Then we can ask about the diverging case. This time, we’ll say that the smaller series, \(\displaystyle \sum_{k=0}^\infty a_k\) diverges.
🔗
A sequence of green dots, labeled {partial sum of b_k}, increasing to seemingly infinity. There is a second sequence of red dots, labeled {partial sums of a_k}, also increasing to seemingly infinity, but below the green dots.
Figure 8.7.3. Comparison of partial sums when \(\displaystyle\sum_{k=0}^\infty a_k\) diverges.
🔗
We can think that this “smaller” sequence of partial sums is “pushing” the “larger” sequence of partial sums up to infinity with it.
🔗
These two cases make up our first comparison mechanic between two infinite series.
🔗
At the end of Section 8.6 Common Series Types, we referenced the series:
\begin{equation*} \sum_{k=0}^\infty \frac{1}{k^3+1}\text{.} \end{equation*}
Let’s use our new test!
🔗

Example 8.7.5.

Does the series \(\displaystyle \sum_{k=0}^\infty \frac{1}{k^3+1}\) converge or diverge? How do you know?
🔗
Hint 1.
If we’re going to use our new Direct Comparison Test, we need to identify two things:
  1. Some intuition on whether we think our series converges or not.
    🔗
    🔗
  2. An appropriate series to compare to. Likely, this will be either a Geometric Series or a \(p\)-Series, since we have clear convergence criteria for each of those.
    🔗
    🔗
We can do this in any order: sometimes we might use the structure of the series we’re looking at to give us a good candidate to compare to, and that might tell us the behavior we think we’re looking for. Other times we might have good intuition about convergence/divergence of the series which will tell us whether we need to find a series that is smaller or larger to compare to.
🔗
What do you think? Do we have a suitable comparison?
🔗
🔗
Hint 2.
Compare to the \(p\)-Series \(\displaystyle \sum_{k=1}^\infty \frac{1}{k^3}\text{.}\) Here, \(p=3\text{.}\) Based on this, do we need to show that \(\dfrac{1}{k^3+1}\) is greater than or less than \(\dfrac{1}{k^3}\text{?}\)
🔗
Show this!
🔗
Does the change in the starting index matter?
🔗
🔗
Solution.
Let’s compare our series to the converging \(p\)-series with \(p=3\text{:}\)
\begin{equation*} \sum_{k=0}^\infty \frac{1}{k^3+1}\sim \sum_{k=1}^\infty \frac{1}{k^3}\text{.} \end{equation*}
We want to show that \(\dfrac{1}{k^3+1}\leq \dfrac{1}{k^3}\) for \(k\geq 1\text{.}\)
🔗
Let’s start with comparing the denominators, and move from there.
\begin{equation*} k^3+1 \gt k^3 \text{ for any value of } k \end{equation*}
Now we can think about reciprocals:
\begin{equation*} \frac{1}{k^3+1} \lt \frac{1}{k^3} \text{ for all } k\geq 1\text{.} \end{equation*}
This means that, since \(\displaystyle \sum_{k=1}^\infty \frac{1}{k^3}\) converges, then \(\displaystyle\sum_{k=1}^\infty \frac{1}{k^3+1}\) must also converge.
🔗
We can just add the term where \(k=0\) to get
\begin{align*} \sum_{k=0}^\infty \frac{1}{k^3+1} \amp = \overbrace{\frac{1}{0^3+1}}^{k=0} + \sum_{k=1}^\infty \frac{1}{k^3+1}\\ \amp = 1 + \sum_{k=1}^\infty \frac{1}{k^3+1} \end{align*}
So then we know that our series, \(\displaystyle\sum_{k=0}^\infty \frac{1}{k^3+1}\) must converge.
🔗
🔗
🔗
A quick note: in this example, we thought about building the link
\begin{equation*} \sum_{k=1}^\infty \frac{1}{k^3+1} \sim \sum_{k=1}^\infty \frac{1}{k^3} \end{equation*}
and then arguing that changing the index to start at \(k=0\) by adding in a single term wouldn’t change the behavior of the infinite series.
🔗
In general, we don’t need to add in that last argument. We can assume from here on out that changing our starting index won’t impact the behavior of the series (as long as we’re avoiding things like division by 0 and such). So showing that \(\dfrac{1}{k^3+1}\lt \dfrac{1}{k^3}\) for \(k\geq 1\) is enough for us!
🔗
🔗

Subsection (Un)Helpful Comparisons

Activity 8.7.2. (Un)Helpful Comparisons.

We’re going to consider a handful of infinite series, here:
  1. \(\displaystyle \displaystyle \sum_{k=1}^\infty \frac{2}{k(3^k)}\)
    🔗
    🔗
  2. \(\displaystyle \displaystyle \sum_{k=3}^\infty \frac{\sqrt{k+1}}{k-2}\)
    🔗
    🔗
🔗
(a)
Pick a series that is reasonable to use as a comparison for each of the series listed. Remember, we want:
  • A series that is recognizable (probably a Geometric Series or a \(p\)-Series), so that we know the behavior of it: we need to know whether the series we’re comparing to converges or diverges!
    🔗
    🔗
  • A series that is similar enough to the series we’re working with that we can construct an inequality comparing the term structure. It can be hard to compare functions that are seemingly unrelated to each other!
    🔗
    🔗
  • A series that has terms that are either larger or smaller than our series, depending on whether we are trying to show that our series converges or diverges.
    🔗
    🔗
🔗
Hint 1.
It can be useful to think about what the dominating pieces of each term structure are. What parts of the function will be most important, especially as the index, \(k\text{,}\) gets larger?
🔗
🔗
Hint 2.
  1. In the denominator, think about \(k\) contrasted with \(3^k\text{.}\) Which of these will be more influential in determining the value of the term when \(k\) gets large?
    🔗
    🔗
  2. In the numerator, think about \(k\) contrasted with \(+1\) under the square root. Which of these will be more influential? In the denominator, contrast \(k\) and \(-2\text{.}\) Which of these will be more influential? What does this fraction look like when we just consider the numerator and denominator’s most dominant pieces?
    🔗
    🔗
🔗
🔗
Solution.
  1. Let’s link the following two series using a comparison:
    \begin{equation*} \sum_{k=1}^\infty \frac{2}{k(3^k)} \sim \sum_{k=1}^\infty \frac{2}{3^k}\text{.} \end{equation*}
    We can notice that \(\displaystyle \sum_{k=1}^\infty \frac{2}{3^k}\) is a geometric series with \(a=\dfrac{2}{3}\) and \(r=\dfrac{1}{3}\text{.}\) It converges!
    🔗
    (Specifically, this series converges to 1.)
    🔗
    🔗
  2. Let’s link the following two series using a comparison:
    \begin{equation*} \sum_{k=3}^\infty \frac{\sqrt{k+1}}{k-2} \sim \sum_{k=3}^\infty \frac{\sqrt{k}}{k} = \sum_{k=3}^\infty \frac{1}{\sqrt{k}}\text{.} \end{equation*}
    Note that \(\displaystyle \sum_{k=3}^\infty \frac{1}{\sqrt{k}}\) is a diverging \(p\)-series, since \(p=\dfrac{1}{2}\text{.}\)
    🔗
    🔗
🔗
🔗
🔗
(b)
Build the comparison from the series we start with to the one you picked. What kinds of conclusions can you make?
🔗
Hint.
  1. When we compare \(\dfrac{2}{k(3^k)}\) with \(\dfrac{2}{3^k}\text{,}\) we can start with the denominator. What does multiplying by \(k\) do to the value of \(3^k\text{?}\) It might help to write some of the values out for \(k=1, 2, 3,...\)
    🔗
    🔗
  2. When we compare \(\dfrac{\sqrt{k+1}}{k-2}\) with \(\dfrac{\sqrt{k}}{k}\text{,}\) we can think of the numerator and denominator separately. What does adding 1 under the square root do to the value of \(\sqrt{k}\text{?}\) What does subtracting 2 in the denominator do to \(k\text{?}\) How do these impact the fraction?
    🔗
    🔗
🔗
🔗
Solution.
  1. Since \(k\geq 1\text{,}\) we can say that
    \begin{equation*} k(3^k) \geq 3^k \text{ for } k=1,2,3, ... \end{equation*}
    This means that
    \begin{equation*} \frac{1}{k(3^k)}\leq \frac{1}{3^k} \text{ for } k=1,2,3,... \end{equation*}
    since a big denominator leads to a small fraction. Then, we can scale both by a factor of 2:
    \begin{equation*} \frac{2}{k(3^k)}\leq \frac{2}{3^k} \text{ for } k=1,2,3,... \end{equation*}
    🔗
    Since \(\displaystyle \sum_{k=1}^\infty \frac{2}{3^k}\) is a converging geometric series (since \(r=\frac{1}{3}\) and so \(|r|\lt 1\)), then we can say that \(\displaystyle \sum_{k=1}^\infty \frac{2}{k(3^k)}\) must also converge.
    🔗
    🔗
  2. We can see that \(k-2 \lt k\text{.}\) Then, when we think about reciprocals, we see that
    \begin{equation*} \frac{1}{k-2}\gt \frac{1}{k} \text{ for } k\gt 2 \end{equation*}
    since a small denominator leads to a big fraction. Then, we can multiply both by \(\sqrt{k}\text{:}\)
    \begin{equation*} \frac{\sqrt{k}}{k-2} \gt \frac{\sqrt{k}}{k}\text{.} \end{equation*}
    Finally, since \(k+1 \gt k\text{,}\) we know that \(\sqrt{k+1}\gt \sqrt{k}\text{.}\)
    🔗
    This means that:
    \begin{equation*} \frac{\sqrt{k+1}}{k-2} \gt \frac{\sqrt{k}}{k-2} \gt \frac{\sqrt{k}}{k}\text{.} \end{equation*}
    So, we have that \(\dfrac{\sqrt{k+1}}{k-2} \gt \dfrac{1}{\sqrt{k}}\) for \(k= 3, 4, 5, ...\)
    🔗
    Since \(\displaystyle \sum_{k=3}^\infty \frac{1}{\sqrt{k}}\) is a diverging \(p\)-series (since \(p=\frac{1}{2}\leq 1\)), then \(\displaystyle \sum_{k=3}^\infty \frac{\sqrt{k+1}}{k-2}\) must also diverge.
    🔗
    🔗
🔗
🔗
🔗
(c)
We’re going to change the series we’re considering to two slightly different series:
  1. \(\displaystyle \displaystyle \sum_{k=1}^\infty \frac{2k}{3^k}\)
    🔗
    🔗
  2. \(\displaystyle \displaystyle \sum_{k=3}^\infty \frac{\sqrt{k-1}}{k+2}\)
    🔗
    🔗
How do these small changes impact the inequalities you built?
🔗
Hint.
  1. We moved \(k\) from the denominator to the numerator. If the numerator is the thing getting bigger, how does that impact the size of this fraction in the same comparison as before?
    🔗
    🔗
  2. We changed the signs: we’re subtracting in the numerator and adding in the denominator. How does that impact the size of this fraction in the same comparison as before?
    🔗
    🔗
🔗
🔗
Solution.
  1. Since \(k\geq 1\text{,}\) we know that \(2k\geq 2\text{.}\) This means that
    \begin{equation*} \frac{2k}{3^k} \geq \frac{2}{3^k} \text{ for } k=1,2,3,... \end{equation*}
    🔗
    🔗
  2. We have \(k+2 \gt k\text{,}\) and so:
    \begin{equation*} \frac{1}{k+2}\lt \frac{1}{k} \text{ for } k=3,4,5... \end{equation*}
    This means that:
    \begin{equation*} \frac{\sqrt{k}}{k+2} \lt \frac{1}{\sqrt{k}} \text{ for } k=3,4,5... \end{equation*}
    Finally, since \(\sqrt{k-1}\lt \sqrt{k}\text{,}\) we have:
    \begin{equation*} \frac{\sqrt{k-1}}{k+2} \lt \frac{1}{\sqrt{k}} \text{ for } k=3,4,5... \end{equation*}
    🔗
    🔗
🔗
🔗
🔗
(d)
How do these changes in the inequalities change the conclusions we can draw from the Direct Comparison Test?
🔗
Solution.
In both cases, the Direct Comparison Test is inconclusive. This means that we cannot conclude that either of these series converges or diverges: we don’t have enough information to justify any claim we might make.
🔗
🔗
🔗
(e)
What do you think is happening with these series: do you think that these small changes are enough to change the behavior of the series (i.e. whether it converges or diverges)?
🔗
🔗
🔗
There are some ways around this. When we find a comparison that we think is reasonable, but has the wrong inequality for us to make a conclusion, we can do one of two things:
  1. Try a different comparison.
    🔗
    🔗
  2. Try a different test.
    🔗
    🔗
We’ll address the second strategy momentarily.
🔗

Note 8.7.6.

In fact, we might argue that we could start with a different test! It might be more useful to skip using the Direct Comparison Test in favor of just using the Limit Comparison Test, which we’ll see soon, or the Ratio Test or Root Test, which we’ll talk about in the next section.
🔗
I think that the only real reason to think about the Direct Comparison Test is that
  • Sometimes it can be pretty quick to use. Sometimes.
    🔗
    🔗
  • It is much easier to see why it works, since we can make a nice argument about monotonic and bounded sequences of partial sums. From there, the Limit Comparison Test (coming up next) isn’t a big jump conceptually. But it might be harder to start with.
    🔗
    🔗
🔗
🔗
So let’s think about one of the series from Activity 8.7.2:
\begin{equation*} \sum_{k=1}^\infty \frac{2k}{3^k} \end{equation*}
We, intuitively, tried to compare this a related geometric series:
\begin{equation*} \sum_{k=1}^\infty \frac{2k}{3^k} \sim \underbrace{\sum_{k=1}^\infty \frac{2}{3^k}}_{\text{converges}} \end{equation*}
Unfortunately, we weren’t able to make this connection, since \(\dfrac{2k}{3^k} \geq \dfrac{2}{3^k}\) for \(k=1,2,3\ldots\)
🔗
We could, instead, still think that this is a converging series but compare it to the converging \(p\)-series, \(\displaystyle \sum_{k=1}^\infty \frac{1}{k^2}\text{.}\) We’ll actually compare it to \(\displaystyle \sum_{k=1}^\infty \frac{2}{k^2}\text{,}\) but this will converge as well (since the coefficient will just scale the value that the series converges to).
🔗
Note, first, that \(3^k \geq k^3\) for \(k\geq 3\text{.}\) At \(k=3\) we have \(3^3=3^3\text{,}\) but after this intersection point, the exponential will be larger than the power function.
\begin{align*} 3^k \amp \geq k^3 \text{ for } k=3,4,5,...\\ \frac{1}{3^k} \amp \leq \frac{1}{k^3} \text{ for } k=3,4,5...\\ \frac{2k}{3^k} \amp \leq \frac{2k}{k^3} \text{ for } k=3,4,5...\\ \frac{2k}{3^k} \amp \leq \frac{2}{k^2} \text{ for } k=3,4,5... \end{align*}
And there we go! We have \(\dfrac{2k}{3^k} \leq \dfrac{2}{k^2}\) for \(k=3,4,5...\) and \(\displaystyle \sum_{k=3}^\infty \frac{2}{k^2}\) converges, so then \(\displaystyle \sum_{k=3}^\infty \frac{2k}{3^k}\) must also converge.
🔗
Of course, we can add two more real numbers (when \(k=1\) and \(k=2\)), and the resulting series will still converge. So, \(\displaystyle \sum_{k=1}^\infty \frac{2k}{3^k}\) converges, just like we originally thought.
🔗
Let’s not get ahead of ourselves: this quick change from one comparison to another is rarely easy! Here are some questions we can ask:
  • Where did \(\displaystyle\sum_{k=1}^\infty \frac{1}{k^2}\) come from? How could we have anticipated that as being useful?
    🔗
    🔗
  • Didn’t we think, originally, that this was almost a geometric series? Why are we switching to comparing to a \(p\)-series?
    🔗
    🔗
  • Is there some systematic way for us to think about what to compare to? Something other than appealing to growth rates?
    🔗
    🔗
These questions will remain largely unanswered in this text, other than the following (unhelpful) solution: getting good at thinking about inequalities and comparisons means that inequalities and comparisons become easier.
🔗
This is not intended to be a self-indulged brag: I am not that good at thinking about inequalities and comparisons either! It’s just meant to have you confront the fact that this test, while understandable, is not always useful in practice. There are better paths forward!
🔗
Let’s follow those instead.
🔗
🔗

Subsection Limit Comparison

Let’s revisit some of our intuition from earlier. When we talked about the series in Example 8.7.5, we made the claim that it probably acted like the \(p\)-series \(\displaystyle \sum_{k=1}^\infty \frac{1}{k^3}\text{.}\) Why did we choose this series?
🔗
Similarly, how did we pick our comparisons in Activity 8.7.2?
🔗
We had thought about what parts of the functions defining the terms of the series would take over as \(k\to\infty\text{.}\) We were thinking about which parts of these terms ends up dominating, in behavior, over the other parts.
🔗
We’re thinking about limits, really!
🔗
We’re going to use this intuition that we have about limits and relative growth rates to come up with another way of thinking about whether two things act similarly. There are a few ways that we could approach this, but it will be useful to think about this comparison of relative growth rates as ratios.
🔗
What if we think about the ratio of the functions defining the terms of the series we’re comparing, and see how this ratio acts in the limit as \(k\to\infty\text{?}\)
🔗

Activity 8.7.3. Ratios for Comparison.

Let’s start with some functions: we’ll consider \(f(x)\) and \(g(x)\) as two functions that are continuous when \(x\geq 0\) with \(f(x)\to 0\) and \(g(x)\to 0\) as \(x\to\infty\text{.}\)
🔗
All of this is so that we can think about \(\dfrac{f(x)}{g(x)}\) and know that we have an indeterminate form. We could put the requirement of differentiability on these functions (so that we could think about L’Hôpital’s Rule), but we don’t need to do that.
🔗
We’re going to now consider the limit:
\begin{equation*} \lim_{x\to\infty} \frac{f(x)}{g(x)}\text{.} \end{equation*}
🔗
(a)
What would the limit \(\displaystyle \lim_{x\to\infty} \frac{f(x)}{g(x)}\) look like if \(g(x)\to 0\) with a faster growth rate than \(f(x)\) does? In this case, we might say that:
\begin{equation*} f(x) \gt \gt g(x)\text{.} \end{equation*}
🔗
Hint.
What does it normally look like when a fraction of numbers has a very small denominator compared to the numerator?
🔗
🔗
🔗
(b)
What would the limit \(\displaystyle \lim_{x\to\infty} \frac{f(x)}{g(x)}\) look like if \(f(x)\to 0\) with a faster growth rate than \(g(x)\) does? In this case, we might say that:
\begin{equation*} g(x) \gt \gt f(x)\text{.} \end{equation*}
🔗
Hint.
What does it normally look like when a fraction of numbers has a very large denominator compared to the numerator?
🔗
🔗
🔗
(c)
If the functions \(f(x)\) and \(g(x)\) eventually act equivalently, then what does the limit \(\displaystyle \lim_{x\to\infty} \frac{f(x)}{g(x)}\) look like?
🔗
Hint 1.
When we say that these two functions act equivalently, we might mean that while they both approach 0 in the limit, they do it in the same way, or with identical growth rates.
🔗
🔗
Hint 2.
What does it normally look like when a fraction of numbers is something over an equivalent thing?
🔗
🔗
🔗
(d)
If the function \(f(x)\) eventually acts like some scaled version of \(g(x)\text{,}\) then what does the limit \(\displaystyle \lim_{x\to\infty} \frac{f(x)}{g(x)}\) look like?
🔗
Hint.
We can think that \(f(x)\to L(g(x))\) as \(x\to\infty\) for some real number \(L\text{.}\)
🔗
🔗
🔗
🔗
So we have three outcomes of our comparisons using ratios of functions in the limit:
  1. The numerator function could, eventually, be so much larger than the denominator function that the limit of the ratio is infinite.
    🔗
    🔗
  2. The denominator could, eventually, be so much larger than the numerator function that the limit of the ratio is zero.
    🔗
    🔗
  3. The numerator and denominator could, eventually, act so similarly to each other (or like scaled versions of each other) that the limit is some real number that isn’t 0.
    🔗
    🔗
This is the motivation for the next comparison test! We’ll just think about the functions defining the terms of a series instead, and we’ll make conclusions about the series themselves instead of the functions defining the terms.
🔗

Example 8.7.8.

For each of the following infinite series, try to select an appropriate comparison series, and then apply a comparison test to make conclusions about whether the series converges or diverges.
🔗
(a)
\(\displaystyle \sum_{k=1}^\infty \frac{e^{1/k}}{\sqrt{k^2+k}}\)
🔗
Hint 1.
What happens, in the limit as \(k\to\infty\) to \(e^{1/k}\text{?}\) How does \(\sqrt{k^2+k}\) act in the limit: does the \(k\) term influence much, compared to \(k^2\text{?}\)
🔗
🔗
Hint 2.
One of the comparisons we can try is to link the behavior of these two series:
\begin{equation*} \sum_{k=1}^\infty \frac{e^{1/k}}{\sqrt{k^2+k}} \sim \sum_{k=1}^\infty \frac{1}{\sqrt{k^2}} = \sum_{k=1}^\infty \frac{1}{k}\text{.} \end{equation*}
🔗
🔗
Solution.
In order to link these series, we’ll apply a limit comparison test:
\begin{equation*} \sum_{k=1}^\infty \frac{e^{1/k}}{\sqrt{k^2+k}} \sim \sum_{k=1}^\infty \frac{1}{\sqrt{k^2}} = \sum_{k=1}^\infty \frac{1}{k}\text{.} \end{equation*}
So let’s investigate the limit of the ratio of the terms.
\begin{align*} \lim_{k\to\infty} \frac{\left(\frac{e^{1/k}}{\sqrt{k^2+k}}\right)}{\left(\frac{1}{k}\right)} \amp = \lim_{k\to\infty} \left(\frac{e^{1/k}}{\sqrt{k^2+k}}\right)\left(\frac{k}{1}\right)\\ \amp = \lim_{k\to\infty} \frac{ke^{1/k}}{\sqrt{k^2+k}}\\ \amp = \left(\underbrace{\lim_{k\to\infty} e^{1/k}}_{\to e^0 = 1} \right)\left(\lim_{k\to\infty} \frac{k}{\sqrt{k^2+k}}\right)\\ \amp = \lim_{k\to\infty} \frac{k}{\sqrt{k^2+k}} \end{align*}
This limit is one that we can think about using Theorem 1.4.7: we can apply the limit in the denominator under the root, and notice that the whole thing is really dependent on the behavior of \(k^2\text{.}\)
🔗
We’ll apply a technique that is used in the proof of the theorem.
\begin{align*} \lim_{k\to\infty} \frac{k}{\sqrt{k^2+k}}\amp = \lim_{k\to\infty} \frac{k}{\sqrt{k^2\left(1+\frac{k}{k^2}\right)}}\\ \amp = \lim_{k\to\infty} \frac{k}{\sqrt{k^2}\sqrt{1+\frac{1}{k}}}\\ \amp = \lim_{k\to\infty} \frac{k}{k\sqrt{1+\frac{1}{k}}}\\ \amp = \lim_{k\to\infty} \frac{1}{\sqrt{1+\frac{1}{k}}} \end{align*}
Now, since \(\dfrac{1}{k}\to 0\) as \(k\to\infty\) we end up with:
\begin{equation*} \lim_{k\to\infty} \frac{\left(\frac{e^{1/k}}{\sqrt{k^2+k}}\right)}{\left(\frac{1}{k}\right)} = 1\text{.} \end{equation*}
Conclusions: Since we’re comparing our series to the diverging \(p\)-series \(\displaystyle\sum_{k=1}^\infty \frac{1}{k}\text{,}\) and the limit comparison test says that these two infinite series must have the same behavior (since the limit of the ratio of the term functions was 1), then we can conclude that the infinite series \(\displaystyle \sum_{k=1}^\infty \frac{e^{1/k}}{\sqrt{k^2+k}}\) also diverges.
🔗
🔗
🔗
(b)
\(\displaystyle\sum_{k=0}^\infty \frac{1}{k!}\)
🔗
Hint.
This is a hard one to come up with a reasonable comparison. Try writing out some terms and getting a feel for what kinds of things are happening structurally:
  • Is there something you can describe, recursively, about how we get from one term in the series to the next?
    🔗
    🔗
  • Are there consistent operations that we’re applying to terms?
    🔗
    🔗
  • Does this remind you of anything?
    🔗
    🔗
🔗
🔗
Solution.
We can compare this to a converging geometric series, \(\displaystyle\sum_{k=0}^\infty \frac{1}{2^k}\text{.}\) So, we want to draw the following link:
\begin{equation*} \sum_{k=0}^\infty \frac{1}{k!} \sim \sum_{k=0}^\infty \frac{1}{2^k}\text{.} \end{equation*}
The limit comparison test follows as such:
\begin{align*} \lim_{k\to\infty} \frac{\left(\frac{1}{k!}\right)}{\left(\frac{1}{2^k}\right)} \amp = \lim_{k\to\infty} \frac{2^k}{k!} \end{align*}
We cannot use L’Hopital’s Rule here, since \(k!\) is not a continuous function for real numbers (since it only takes in non-negative integer inputs) and so it is not differentiable.
🔗
We can, instead, appeal to growth rates: \(k!\) approaches infinity much faster than \(2^k\text{,}\) and so this fraction has a much larger denominator.
\begin{equation*} \lim_{k\to\infty} \frac{2^k}{k!} = 0\text{.} \end{equation*}
Conclusions: By the Limit Comparison Test, this means that \(\frac{1}{k!} \lt \lt \frac{1}{2^k}\text{,}\) and so, since \(\displaystyle\sum_{k=0}^\infty \frac{1}{2^k}\) is a converging geometric series, then the infinite series \(\displaystyle \sum_{k=0}^\infty \frac{1}{k!}\) must also converge.
🔗
🔗
🔗
🔗
There isn’t anything special about the series we’re comparing to: We could have used any mix of the following comparisons to find the same conclusions:
  • \(\displaystyle \displaystyle \sum_{k=1}^\infty \frac{e^{1/k}}{\sqrt{k^2+k}} \sim \sum_{k=1}^\infty \frac{1}{\sqrt{k}}\)
    🔗
    🔗
  • \(\displaystyle \displaystyle \sum_{k=0}^\infty \frac{1}{k!} \sim \sum_{k=1}^\infty \frac{1}{k^2}\)
    🔗
    🔗
  • \(\displaystyle \displaystyle \sum_{k=0}^\infty \frac{1}{k!} \sim \sum_{k=1}^\infty \frac{1}{10^k}\)
    🔗
    🔗
There’s no magic series to compare to: one of the nice things about the limit comparison test is that we can compare a series to another one not based on similar structure, but based on intuited behavior: if you think a series converges, compare it to a converging \(p\)-series if you’d like!
🔗
There certainly are some instances where it is reasonable to pick a specific series to compare to based on the structure.
🔗

Example 8.7.9.

Consider the following series:
\begin{equation*} \sum_{k=1}^\infty \frac{2k^2-k+3\sqrt{k}}{3k^{7/3}+4k^{5/3} - k^{2/5}}\text{.} \end{equation*}
Perform a test and state a conclusion about whether or not this series converges.
🔗
Hint 1.
There are a lot of power functions here! Which ones do you think are most important in deciding how quickly the terms approach 0?
🔗
🔗
Hint 2.
This isn’t a \(p\)-Series, but it might act like one. Compare it to a relevant \(p\)-Series!
🔗
🔗
Solution.
We can note that the numerator is really driven by the quadratic term, \(k^2\text{,}\) while the denominator’s behavior is determined by \(k^{7/3}\text{,}\) the power function with the highest exponent. We can make the following comparison:
\begin{align*} \sum_{k=1}^\infty \frac{2k^2-k+3\sqrt{k}}{3k^{7/3}+4k^{5/3} - k^{2/5}} \amp \sim \sum_{k=1}^\infty \frac{k^2}{k^{7/3}}\\ \amp \sim \sum_{k=1}^\infty \frac{1}{k^{1/3}} \end{align*}
Note that this is a diverging \(p\)-series, and so, in performing this comparison, we think that our series also converges. Let’s show this using a limit comparison.
\begin{align*} \lim_{k\to\infty} \frac{\left(\frac{1}{k^{1/3}}\right)}{\left(\frac{2k^2-k+3\sqrt{k}}{3k^{7/3}+4k^{5/3} - k^{2/5}}\right)} \amp = \lim_{k\to\infty} \left(\frac{1}{k^{1/3}}\right)\left(\frac{3k^{7/3}+4k^{5/3} - k^{2/5}}{2k^2-k+3\sqrt{k}}\right) \\ \amp = \lim_{k\to\infty} \frac{3k^{7/3}+4k^{5/3} - k^{2/5}}{2k^{7/3}-k^{4/3}+3k^{5/6}}\\ \amp = \frac{3}{2} \end{align*}
e\(Conclusion:\) Since this limit is a non-zero real number, we can conclude that our two series have the same behavior. So, since \(\displaystyle \sum_{k=1}^\infty \frac{1}{k^{1/3}}\) diverged, then we know that the series \(\displaystyle \sum_{k=1}^\infty \frac{2k^2-k+3\sqrt{k}}{3k^{7/3}+4k^{5/3} - k^{2/5}}\) must also diverge.
🔗
🔗
🔗
This example is not unique! Note that out selection of the \(p\)-series to use as comparison is based on what we know will happen in the limit that we eventually use in the test itself!
🔗

Note 8.7.11.

We can extend this result pretty easily by loosening up the “rational function” requirement. If we have combinations of power functions (even with non-integer exponents), this works as well!
🔗
🔗
🔗
So we have a great tool for analyzing series that look similar to \(p\)-series: as long as the most aggressive pieces of our terms are defined by power functions, then we can connect the series to the relevant \(p\)-series and use the same convergence criteria through arguments about the degrees of these power functions.
🔗
What about infinite series that are seemingly not connected to a \(p\)-series? We saw other series in this section that acted more like a geometric series:
  • \(\displaystyle \displaystyle \sum_{k=1}^\infty \frac{2}{k(3^k)}\)
    🔗
    🔗
  • \(\displaystyle \displaystyle \sum_{k=1}^\infty \frac{2k}{3^k}\)
    🔗
    🔗
  • \(\displaystyle \displaystyle \sum_{k=1}^\infty \frac{1}{k!}\)
    🔗
    🔗
We can set up some comparisons, like we did in this section, for each of these series individually. But is there a result similar to Theorem 8.7.10 for series that act like a geometric series?
🔗
It turns out that the answer is a resounding, “Yes!” We just need to think about what aspects of a geometric series we’re looking for.
🔗

Practice Problems Practice Problems

1.

For a series \(\sum a_k\) where all of the terms \(a_k\) are positive, explain whether the series converges, diverges, or if we cannot tell based on the following comparisons.
🔗
(a)
\(a_k \lt \frac{1}{k^2}\) for all \(k\) .
🔗
🔗
(b)
\(a_k \gt \frac{1}{k^2}\) for all \(k\) .
🔗
🔗
(c)
\(a_k \lt \frac{1}{k}\) for all \(k\) .
🔗
🔗
(d)
\(a_k \gt \frac{1}{k}\) for all \(k\) .
🔗
🔗
(e)
\(a_k \lt 1\) for all \(k\) .
🔗
🔗
(f)
\(a_k \gt 1\) for all \(k\) .
🔗
🔗
🔗

2.

For each pair of series, compare the terms of each with either \(\lt\) or \(\gt\text{.}\) What does the Direct Comparison Test say about the first series in each pair (if anything)?
🔗
(a)
\(\displaystyle \sum_{k=1}^\infty \left(\frac{1}{\sqrt{k^3+1}}\right)\) compared with \(\displaystyle \sum_{k=1}^\infty \left(\frac{1}{k^{3/2}}\right)\)
🔗
🔗
(b)
\(\displaystyle \sum_{k=1}^\infty \left(\frac{1}{k^24^k}\right)\) compared with \(\displaystyle \sum_{k=1}^\infty \left( \frac{1}{4^k} \right)\)
🔗
🔗
(c)
\(\displaystyle \sum_{k=2}^\infty \left(\frac{k+1}{(k-1)^2}\right)\) compared with \(\displaystyle \sum_{k=2}^\infty\left(\frac{1}{k}\right)\)
🔗
🔗
(d)
\(\displaystyle \sum_{k=1}^\infty \left(\frac{1}{k!}\right)\) compared with \(\displaystyle \sum_{k=1}^\infty \left( \frac{1}{k^2} \right)\)
🔗
🔗
🔗

3.

What is an advantage of using the Limit Comparison Test instead of the Direct Comparison Test? Demonstrate this with a specific example.
🔗
🔗

4.

For each pair of series, attempt to compare the terms with either \(\lt\) or \(\gt\) . Explain why the Direct Comparison Test fails (or explain why the comparison is difficult), and then apply the Limit Comparison Test, and explain the conclusions.
🔗
(a)
\(\displaystyle \sum_{k=1}^\infty \left(\frac{1}{\sqrt{k+1}}\right)\) compared with \(\displaystyle \sum_{k=1}^\infty \left(\frac{1}{k^{1/2}}\right)\)
🔗
🔗
(b)
\(\displaystyle \sum_{k=1}^\infty \left(\frac{k-1}{(k+1)^2}\right)\) compared with \(\displaystyle \sum_{k=1}^\infty\left(\frac{1}{k}\right)\)
🔗
🔗
(c)
\(\displaystyle \sum_{k=1}^\infty \left(\sqrt{\frac{k}{k^2+1}}\right)\) compared with \(\displaystyle \sum_{k=1}^\infty \left(\frac{1}{\sqrt{k}}\right)\)
🔗
🔗
🔗

5.

For each series below, determine whether the series converges or diverges using either the Direct or Limit Comparison Test.
🔗
(a)
\(\displaystyle \sum_{k=2}^\infty \left( \frac{4k}{k^3-1}\right)\)
🔗
🔗
(b)
\(\displaystyle \sum_{k=1}^\infty \left( \frac{k}{2^k} \right)\)
🔗
🔗
(c)
\(\displaystyle \sum_{k=1}^\infty \left( \frac{3}{\sqrt{k}+\sqrt[3]{k}}\right)\)
🔗
🔗
(d)
\(\displaystyle \sum_{k=2}^\infty \left( \sqrt[4]{\frac{k}{k^4-1}}\right)\)
🔗
🔗
(e)
\(\displaystyle \sum_{k=1}^\infty \left( \frac{1}{\ln(k)} \right)\)
🔗
🔗
(f)
\(\displaystyle \sum_{k=1}^\infty \left( \frac{2}{k^k}\right)\)
🔗
🔗
(g)
\(\displaystyle\sum_{k=1}^\infty \left(\frac{k^3-k+1}{k^{9/2}+4k^2+1}\right)\)
🔗
🔗
(h)
\(\displaystyle\sum_{k=1}^\infty \left(\frac{k^{3/2}+4}{k^{2}-k+\sqrt{k}}\right)\)
🔗
🔗
🔗
🔗
🔗
PrevTopNext